學校教過的數學法則當中,最簡單巧妙的大概就是「三角形的三個角加起來永遠是180度」。永遠是對的,沒有例外,不管是銳角三角形(三個角都小於90度)或鈍角三角形(其中一個角大於90度)、直角三角形、正三角形(三個邊及三個角都相等)、等腰三角形(有兩個邊及兩個角相等),還是不規則三角形(所有的邊與角都不相等)。
但是(你可能會想坐著聽我接下來要講的事),學校騙了你。三角形的三個角加起來不會永遠是180度,而且證據一直在你眼前。
一般人很自然會用歐氏幾何的角度來思考,這是平面上的幾何學,歐幾里得在西元前300年左右確立的。這個理論之所以說得通,是因為在平面紙張上畫幾何圖形,但實際上,地面只是近乎平面,兩者有很明顯的差異。生活在近似球形的地球表面上,傳統歐氏幾何幾乎無用武之地。
「三角形三個內角總和等於180度」這個法則,是歐幾里得第五公設的其中一種說法,第1章曾介紹過這個公設。第五公設的原始說法更複雜些:
若有一線段截兩條直線,在同側形成的兩個內角加起來小於兩個直角的話,則兩直線繼續延長,就會在兩內角總和小於兩個直角的那一側相交。
以上敘述如圖所示。兩條直線與第三條相交,形成的兩個交角都小於90度,表示這兩條線在歐氏平面幾何中一定會相交。
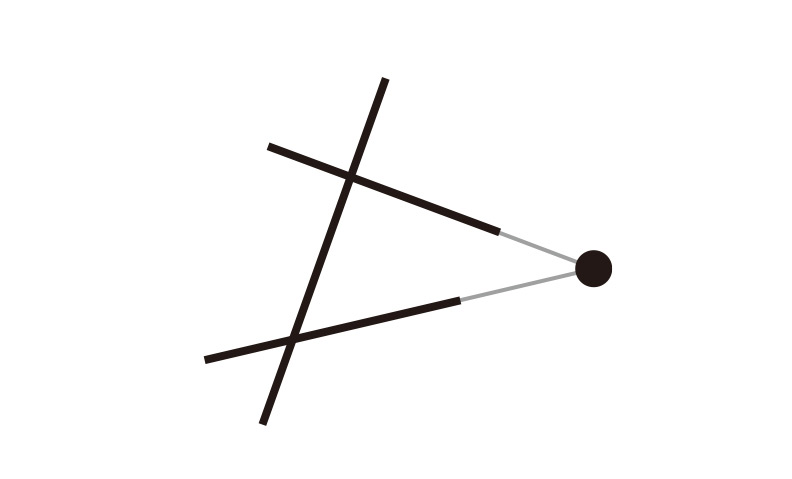
倘若這兩條直線不相交,就會互相平行。歐幾里得的第五公設表示,如果兩直線與第三條線相交且都成直角,則兩直線平行,因此它也稱為平行公設。稍微費一點工夫,就能證明這個說法等同於「三角形的三個角加起來是180度」,前提是三角形位在平面上。
隆起的圓
假設你站在兩條經線之間的一小段赤道上,你眼前的三條線(赤道及兩條經線)都屬於大圓,這些圓弧繞著地球最寬的地方,有最大的半徑(在地球表面上畫不出比這更大的圓了)。大圓也提供了距離最短的路徑。地球上任兩點之間的最短航線,就是這兩點之間的唯一大圓。大圓之於球面幾何,就如直線之於歐氏平面幾何,大圓是距離最短的路徑,因此也應該遵循同樣的法則。
但接下來你會大吃一驚。假如你蹲下來量兩條經線與赤道所成的夾角,會發現兩個角都是直角。可是,這兩條經線就像其他的經線一樣,會在南北兩極交會,彼此不平行。這是人人都熟悉的事物,卻正是平行公設的反例。
球面上的三角形,是由大圓的弧構成,它會往外隆起,三個角加起來超過180度,至於超過多少,要看三角形的大小而定。
若是小三角形,三個角的總和只比180度大一點點,因為就小區域而言,這塊地面近乎平面。但三角形愈大,比方說連接倫敦(英國)、明斯特(德國)、伯斯(澳洲)三地的三角形,三個角的總和也會隨之增加(見下圖)。
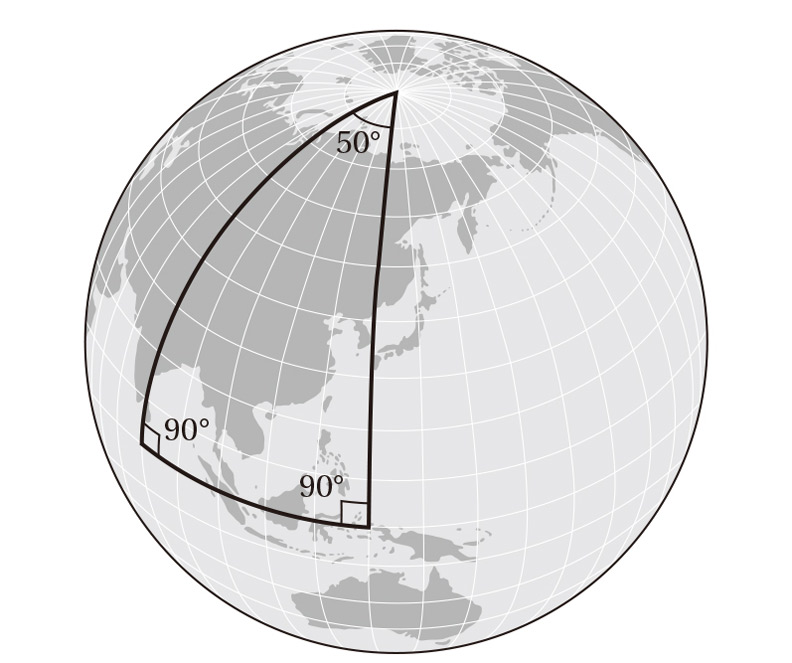
球面幾何與歐氏幾何從地圖上看差異特別明顯,畢竟地圖是把球面描繪在平面紙張上。任何一種平面世界地圖,都有某種程度的扭曲(第60章會談到)。最常使用的地圖繪製法叫做麥卡托投影(Mercator projection),製作出來的地圖在赤道附近相當準確,但靠近兩極的區域,距離及大小會過度放大,格陵蘭看上去比非洲大很多,可實際上它的面積差不多是非洲的十四分之一。

本文節錄自:《數學好有事》一書,瑪莉安.弗萊伯格(Marianne Freiberger)、瑞秋.湯瑪斯(Rachel Thomas)著,畢馨云譯,麥田出版。
圖片來源:pixabay














